2, 弹性模量计算公式中应力、应变分别指什么?
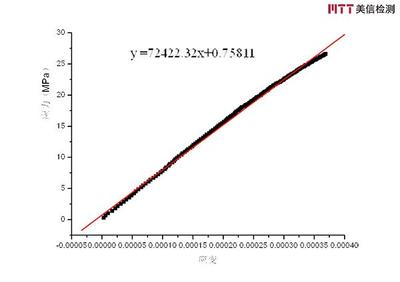
应变是指杆件变形量与总长度的比值,类似于伸长率。应力类似于压强的定义,即单位面积所受的力,计算公式为 σ=F/A。弹性模量是工程材料重要的性能参数,从宏观角度来说,弹性模量是衡量物体抵抗弹性变形能力大小的尺度,从微观角度来说,则是原子、离子或分子之间键合强度的反映。凡影响键合强度的因素均能影响材料的弹性模量,如键合方式、晶体结构、化学成分、微观组织、温度等。因合金成分不同、热处理状态不同、冷塑性变形不同等,金属材料的杨氏模量值会有5%或者更大的波动。但是总体来说,金属材料的弹性模量是一个对组织不敏感的力学性能指标,合金化、热处理(纤维组织)、冷塑性变形等对弹性模量的影响较小,温度、加载速率等外在因素对其影响也不大,所以一般工程应用中都把弹性模量作为常数。弹性模量可视为衡量材料产生弹性变形难易程度的指标,其值越大,使材料发生一定弹性变形的应力也越大,即材料刚度越大,亦即在一定应力作用下,发生弹性变形越小。弹性模量E是指材料在外力作用下产生单位弹性变形所需要的应力。它是反映材料抵抗弹性变形能力的指标,相当于普通弹簧中的刚度。
3, 弹性模量计算公式中的应变是指什么
弹性模量 开放分类: 工程力学 拼音:tanxingmoliang 英文名称:modulusofelasticity 说明:又称杨氏模量。弹性材料的一种最重要、最具特征的力学性质。是物体弹性t变形难易程度的表征。用E表示。定义为理想材料有小形变时应力与相应的应变之比。E以单位面积上承受的力表示,单位为牛/米^2。模量的性质依赖于形变的性质。剪切形变时的模量称为剪切模量,用G表示;压缩形变时的模量称为压缩模量,用K表示。模量的倒数称为柔量,用J表示。 拉伸试验中得到的屈服极限бb和强度极限бS ,反映了材料对力的作用的承受能力,而延伸率δ 或截面收缩率ψ,反映了材料缩性变形的能力,为了表示材料在弹性范围内抵抗变形的难易程度,在实际工程结构中,材料弹性模量E的意义通常是以零件的刚度体现出来的,这是因为一旦零件按应力设计定型,在弹性变形范围内的服役过程中,是以其所受负荷而产生的变形量来判断其刚度的。一般按引起单为应变的负荷为该零件的刚度,例如,在拉压构件中其刚度为: 式中 A0为零件的横截面积。 由上式可见,要想提高零件的刚度E A0,亦即要减少零件的弹性变形,可选用高弹性模量的材料和适当加大承载的横截面积,刚度的重要性在于它决定了零件服役时稳定性,对细长杆件和薄壁构件尤为重要。因此,构件的理论分析和设计计算来说,弹性模量E是经常要用到的一个重要力学性能指标。 在弹性范围内大多数材料服从虎克定律,即变形与受力成正比。纵向应力与纵向应变的比例常数就是材料的弹性模量E,也叫杨氏模量。 弹性模量 在比例极限内,材料所受应力如拉伸,压缩,弯曲,扭曲,剪切等)与材料产生的相应应变之比,用牛/米^2表示 。
4, 大应变和小应变是如何区分的?

大应变就是弹性屈服超过极限, 小应变就是在塑性变形范围之内。“大应变”和“小应变”两者的区别: 1.试验的方法不同。大应变需用吊车吊重锤配合(一般我们在现场看见搭个棚子,检测24小时左右,那就是大应变);小应变用仪器配合手锤敲击即可(弄个仪器在桩头处敲一下那是小应变).PAX 大应变打桩分析仪。 检测时间性:大应变需待砼达到设计强度时方可做,小应变则砼达7天强度时便可做. 2.两者得出的检测数据不同:大应变测出桩的桩身完整性和承载力,而小应变(也叫低应变)则能测桩身完整性。 3.大小应变的能量不同:大应变可以检测出桩身较深处的缺陷,而小应变只能检测出桩顶部分的缺陷。二者都是通过打击桩身,通过返回的信号的连续性来判断桩身的材料的连续性,并以此来判断桩身的质量。
相关概念
弹性模量
一般地讲,对弹性体施加一个外界作用力,弹性体会发生形状的改变(称为“应变”),“弹性模量”的一般定义是:单向应力状态下应力除以该方向的应变。 材料在弹性变形阶段,其应力和应变成正比例关系(即符合胡克定律),其比例系数称为弹性模量。弹性模量的单位是达因每平方厘米。“弹性模量”是描述物质弹性的一个物理量,是一个统称,表示方法可以是“杨氏模量”、“体积模量”等。
变形
变形,是指(1).改变原来的形态。(2).对原来事物的扭曲,亦指被扭曲过的事物。(3).物理学名词。物体受外力作用而产生体积或形状的改变。地面景物的面积、轮廓与其他景物之间的距离、角度等统称景物形状的几何性质。由于地球是一个不规则的曲面,要把这样一个曲面表现到平面上,就会发生裂隙和重叠。
弹性
弹性,经济学名词,由阿尔弗雷德·马歇尔提出,指一个变量相对于另一个变量发生的一定比例的改变的属性。弹性的概念可以应用在所有具有因果关系的变量之间。作为原因的变量通常称作自变量,受其作用发生改变的量称作因变量。例如自变量x和因变量y之间存在关系y = f(x),则y的x弹性:Ey/Ex=(△y/y)/(△x/x)=f"(x)·x/y。












