1, 命题“直角三角形斜边上的中线等于斜边的一半”的逆命题是什么,...
因为这是直角三角形的一种属性,是可以证明的。证法∵a²+b²=c²,且d为斜边的中线,∴对同一个角B,可得:cosB=(a²+c²-b²)/2ac=(a²+1/4c²-d²)/ac化简后为:a²-1/2c²+b²=2d²∵a²+b²=c²,∴代入后可得:1/2c²=2d²,d1=1/2c,d2=-1/2c(不合题意,舍去)∴d=1/2c,命题得证。扩展资料:其逆命题:如果一个三角形一条边的中线等于这条边的一半,那么这个三角形是直角三角形,且这条边为直角三角形的斜边。逆命题是正确的。以该条边的中点为圆心,以中线长为半径作圆,则该边成为圆的直径,该三角形的另一个顶点在圆上,该顶角为圆周角。因为直径上的圆周角是直角,所以逆命题1成立。参考资料来源:百度百科-直角三角形斜边中线定理参考资料来源:百度百科-三角形中线
2, 为什么直角三角形斜边上的中线等于斜边的一半
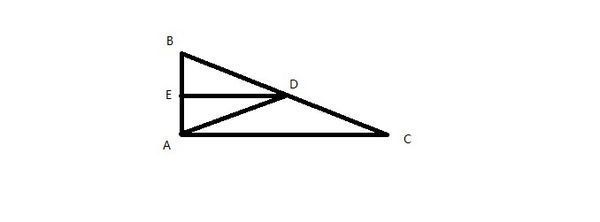
直角三角形斜边中线等于斜边的一半。设在直角三角形ABC中,∠BAC=90°,AD是斜边BC的中线,求证:AD=1/2BC。【证法1】延长AD到E,使DE=AD,连接CE。∵AD是斜边BC的中线,∴BD=CD,又∵∠ADB=∠EDC(对顶角相等),AD=DE,∴△ADB≌△EDC(SAS),∴AB=CE,∠B=∠DCE,∴AB//CE(内错角相等,两直线平行)∴∠BAC+∠ACE=180°(两直线平行,同旁内角互补)∵∠BAC=90°,∴∠ACE=90°,∵AB=CE,∠BAC=ECA=90°,AC=CA,∴△ABC≌△CEA(SAS)∴BC=AE,∵AD=DE=1/2AE,∴AD=1/2BC。取AC的中点E,连接DE。∵AD是斜边BC的中线,∴BD=CD=1/2BC,∵E是AC的中点,∴DE是△ABC的中位线,∴DE//AB(三角形的中位线平行于底边)∴∠DEC=∠BAC=90°(两直线平行,同位角相等)∴DE垂直平分AC,∴AD=CD=1/2BC(垂直平分线上的点到线段两端距离相等)。延长AD到E,使DE=AD,连接BE、CE。∵AD是斜边BC的中线,∴BD=CD,又∵AD=DE,∴四边形ABEC是平行四边形(对角线互相平分的四边形是平行四边形),∵∠BAC=90°,∴四边形ABEC是矩形(有一个角是90°的平行四边形是矩形),∴AE=BC(矩形对角线相等),∵AD=DE=1/2AE,∴AD=1/2BC。

八年级学的,来自人教版八年下册《平行四边形》中的矩形性质。具体内容为:如果一个三角形是直角三角形,那么这个三角形斜边上的中线等于斜边的一半。其逆命题1:如果一个三角形一条边的中线等于这条边的一半,那么这个三角形是直角三角形,且这条边为直角三角形的斜边。逆命题1是正确的。以该条边的中点为圆心,以中线长为半径作圆,则该边成为圆的直径,该三角形的另一个顶点在圆上,该顶角为圆周角。因为直径上的圆周角是直角,所以逆命题1成立。直角三角形除了具有一般三角形的性质外,具有一些特殊的性质:1、直角三角形两直角边的平方和等于斜边的平方。如图,∠BAC=90°,则AB²+AC²=BC²(勾股定理)2、在直角三角形中,两个锐角互余。如图,若∠BAC=90°,则∠B+∠C=90°3、直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。该性质称为直角三角形斜边中线定理。4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
名词解释
CD
承载媒体记录的一种媒介。
90
90(九十)是89与91之间的一个自然数,也是一个偶数。该数除了本身之外,其他约数的和为144>90,因此它是过剩数(盈数)。
AB
Angelababy(1989年2月28日-),本名杨颖,出生于上海市,毕业于嘉诺撒圣心商学书院,中国内地女演员、时尚模特。 Angelababy以模特身份出道,因真人秀《奔跑吧兄弟》赢得广泛关注,凭《鬼吹灯之寻龙诀》获得大众电影百花奖,被誉为“新生代四小花旦”,并多次入选福布斯中国名人榜。












