1, 莫比乌斯环象征什么
象征着循环往复、永恒、无限的。因此常被用于各类标志设计。奇妙之处:一、莫比乌斯环只存在一个面。二、如果沿着莫比乌斯环的中间剪开,将会形成一个比原来的莫比乌斯环空间大一倍的、把纸带的端头扭转了四次再结合的环(并不是莫比乌斯带,在本文中将之编号为:环0),而不是形成两个莫比乌斯环或两个其它形式的环。三、如果再沿着环0的中间剪开,将会形成两个与环0空间一样的、具有正反两个面的环,且这两个环是相互套在一起的,从此以后再沿着环1和环2以及因沿着环1和环2中间剪开所生成的所有环的中间剪开,都将会形成两个与环0空间一样的、具有正反两个面的环,永无止境。
2, 莫比乌斯环的意义是什么
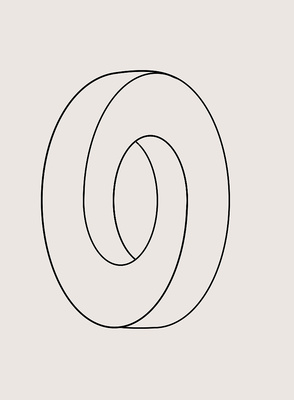
生活中的意义:如果带的两面代表两个独立事物,那莫比乌斯带最大的意义就是象征着融合,既可以代表爱情,宏观上看又可以象征着两个世界的交融,一个星球到达另一个星球是否有这样一条莫比乌斯路。哲学上的意义:1、两面即一面。即矛盾的对立统一。2、沿中线剪开,第一次,得到一个更大的环;第二次及以以后,每次得到两个互相嵌套的环。即世界是普遍联系的。数学上的意义:莫比乌斯带是一种拓展图形,它们在图形被弯曲、拉大、缩小或任意的变形下保持不变,只要在变形过程中不使原来不同的点重合为同一个点,又不产生新点。换句话说,这种变换的条件是:在原来图形的点与变换了图形的点之间存在着一一对应的关系,并且邻近的点还是邻近的点。这样的变换叫做拓扑变换。拓扑有一个形象说法——橡皮几何学。因为如果图形都是用橡皮做成的,就能把许多图形进行拓扑变换。莫比乌斯带是一个二维的紧致流形(即一个有边界的面),可以嵌入到三维或更高维的流形中。它是一个不可定向的的标准范例,可以看作RP#RP。同时也是数学上描绘纤维丛的例子之一。特别地,它是一个有一纤维单位区间,I= [0,1]的圆S上的非平凡丛。仅从莫比乌斯带的边缘看去给出S上一个非平凡的两个点(或Z2)的从。参考资料:百度百科-莫比乌斯带
3, 莫比乌斯指环的奇妙之处

“莫比乌斯带”(板书),为什么呀?是19世纪的几何学家莫比乌斯发现的。很久以前有一个叫莫比乌斯的人,在一个阳光美好的午后,静静的坐在桌前,手中拿着一个长长的纸条,不经意的把纸条拧了一个圈又把两个头对接了起来。也巧,这时正好有一只小蚂蚁到他的桌面上旅游,他微笑着对小蚂说:小朋友,到我这个新建筑上来看看吧。于是小心翼翼地把小蚂蚁请到了手中的纸上,小蚂蚁也许是感到新鲜而又陌生,也就不停的到处游荡,莫比乌斯轻轻的注视着纸上的小蚂蚁,你们猜,他发现了什么?(小蚂蚁虽没翻越任任何一处的纸边沿,却爬过了纸表面的每一个地方。)这让莫比乌斯非常惊讶,这个本来是两个面的纸条经他刚才的一接怎么变成只有一个面了呢?一个伟大的数学发现就这样在不经意间产生了,并且以发现者莫比乌斯的名字命名。所以同学们平时在学好书本知识的同时,要留心观察生活,更多伟大的发明、发现还等着用你们的名字命名呢! 6、关于“莫比乌斯带”还有一个很有趣的故事。据说有一个小偷偷了一位很老实农民的东西,并被当场捕获,将小偷送到县衙,县官发现小偷正是自己的儿子。于是在一张纸条的正面写上:小偷应当放掉,而在纸的反面写了:农民应当关押。县官将纸条交给执事官由他去办理。执事官不想误判此案,但是又不敢得罪县官,你们猜他怎么做?做成“莫比乌斯带”状能改变结果吗?(生猜)现在你们桌上都有县官的这张判决书,请帮执事官想想办法。(生二人小组合作动手操作请个别小组上台演示),聪明的执事官将纸条扭了个弯,用手指将两端捏在一起。然后向大家宣布:根据县太爷的命令放掉农民,关押小偷。县官听了大怒,责问执事官。执事官将纸条捏在手上给县官看,从“应当”二字读起,确实没错。仔细观看字迹,也没有涂改,县官不知其中奥秘,只好自认倒霉。 7、下面再给大家介绍一个关于“莫比乌斯带”的小游戏。宋朝诗人秦少游曾写过一首回形诗:“赏花归去马如飞,去马如飞酒力微,酒力微醒时已暮,醒时已暮赏花归。” (课件显示诗歌)首尾相衔,循环成趣。如果在纸条正面写上“赏花归去马如飞”,再把纸条翻转过来,在背面等距地写上“酒力微醒时已暮”。然后把纸条做成“莫比乌斯带”状,会有什么新发现呢?(顺着这个圈,你就可以反复无穷地读出秦少游的这首诗。) ①艾舍尔《红蚁》:让我们一起来看看蚂蚁在这个“莫比乌斯带”上的运动轨迹吧,由一生上台演示。 ②北京小区科技园“莫比乌斯圈”状阶梯:小朋友在上面玩会发现什么? ③瑞典《不可能的图形》邮票:瑞典1982年发行的一枚邮票,图案是一个古里古怪的图形,如果你用指尖沿着这个古怪的图形上任何一个面顺着一个方向划下去,结果会发现这是一个在现实中不可能造出来的东西。但如果你就这样一直顺着划下去,又会回到原来的出发点,似乎这个物体又不荒谬。其实这是一个立体化的“莫比乌斯圈”。发行这枚“不可能的图形”邮票,意在引导人们关注科学,探索宇宙不解之谜。 ④ 中国科技馆“三叶扭结”:这是中国科技馆的展品,叫“三叶扭结”。它实际上是由“莫比乌斯带”演变而成的,这蓝白相间的灯不停地闪烁,乍看是个漂亮的灯饰,但细瞧,它的特点是什么呀?(只有一面一边)它表示着科学没有国界,各种科学之间没有边界,科学是相互连通的,科学和艺术也是相互连通的意义呢! “莫比乌斯带”听起来确实挺神奇的,但许多事情,都或多或少如此,没有清晰的界限,就如成败,看似截然相反的二个方面,一组反义词。但其实不过是一步之遥。只要你努力,失败的教训会成为成功的基石;如果你骄奢,胜利会转瞬即逝,失败接踵而来。呵呵,原来小小的纸圈上还藏着做人的大道理呢!
4, 莫比乌斯带是什么意思。。??
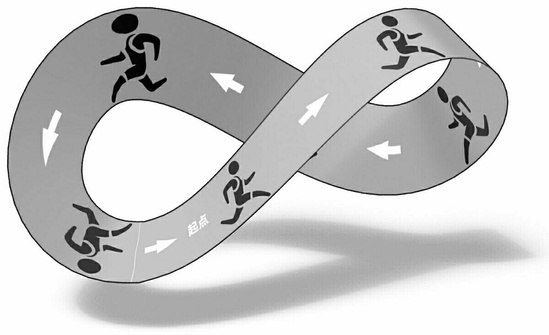
莫比斯环不是象征永恒。莫比斯环也叫做莫比乌斯带,公元1858年,德国数学家莫比乌斯和约翰·李斯丁发现把一根纸条扭转180°后,两头再粘接起来做成的纸带圈,具有魔术般的性质。普通纸带具有两个面,一个正面,一个反面,两个面可以涂成不同的颜色。而这样的纸带只有一个面,一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为莫比乌斯带,意思是说它的曲面只有一个。莫比乌斯带是一种拓展图形,它们在图形被弯曲、拉大、缩小或任意的变形下保持不变,只要在变形过程中不使原来不同的点重合为同一个点,又不产生新点。换句话说,这种变换的条件是:在原来图形的点与变换了图形的点之间存在着一一对应的关系,并且邻近的点还是邻近的点。这样的变换叫做拓扑变换。拓扑有一个形象说法,橡皮几何学。因为如果图形都是用橡皮做成的,就能把许多图形进行拓扑变换。例如一个橡皮圈能变形成一个圆圈或一个方圈。但是一个橡皮圈不能由拓扑变换成为一个阿拉伯数字8。因为不把圈上的两个点重合在一起,圈就不会变成8,莫比乌斯带正好满足了这些要求。参考资料来源:搜狗百科—莫比斯环
名词解释
莫比
莫比,1965年9月11日生于美国纽约哈林区,他的作品始终游走于流行与电子之间,音乐路线迎合了大多数年轻人的聆听品位。他在电子乐界颇有建树,兼任制作人、创作家、DJ,曾是个朋克乐手,甚至还是一家素食餐馆的老板。
图形
图形是指在二维空间中以轮廓为界限的空间碎片,在一个二维空间中可以用轮廓划分出若干的空间形状,图形是空间的一部分,不具有空间的延展性,它是局限的可识别的形状。图形区别于标记、标志与图案,它既不是一种单纯的符号,更不是单一以审美为目的的一种装饰,而是在特定的思想意识支配下的某一个或多个视觉元素组合的一种蓄意的刻画和表达形式。它是有别于词语、文字、语言的视觉形式,可以通过各种手段进行大量复制,是传播信息的视觉形式。













