1, 直角三角形对边比邻边是什么
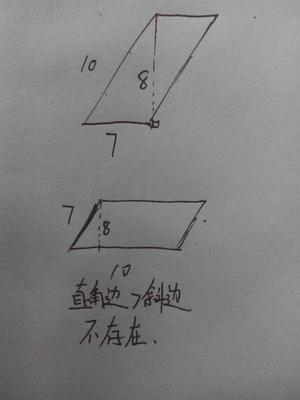
直角三角形对边比邻边是(正切)。在直角三角形中,当平面上的三点A、B、C的连线,AB、AC、BC,构成一个直角三角形,其中∠ACB为直角。对∠BAC而言,对边(opposite)a=BC、斜边(hypotenuse)c=AB、邻边(adjacent)b=AC,则存在以下关系:∠A的对边比斜边=sinA=a/c (即正弦)∠A的邻边比斜边=cosA=b/c(即余弦)∠A的对边比邻边=tanA=a/b(即正切)∠A的邻边比对比=cotA=b/a(即余切)
2, 直角三角形的斜边,对边,邻边分别是哪些边
1、对边。这角的对面的线。2、邻边。这个角的邻居,组成这个角的两条线。3、斜边。直角三角形三条线中最长的这条线。直角三角形的判定2、若a的平方+b的平方=c的平方,则以a、b、c为边的三角形是以c为斜边的直角三角形(勾股定理的逆定理)。3、若一个三角形30°内角所对的边是某一边的一半,那么这个三角形是以这条长边为斜边的直角三角形。 4、两个锐角互余的三角形是直角三角形。 5、证明直角三角形全等时可以利用HL ,两个三角形的斜边长对应相等,以及一个直角边对应相等,则两直角三角形全等。6、若两直线相交且它们的斜率之积互为负倒数,则这两直线垂直。 7、在一个三角形中若它一边上的中线等于这条中线所在边的一半,那么这个三角形为直角三角形。
名词解释
直角三角形
直角三角形是一个几何图形,是有一个角为直角的三角形,有普通的直角三角形和等腰直角三角形两种。 其符合勾股定理,具有一些特殊性质和判定方法。
三角形
三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形,在数学、建筑学有应用。 常见的三角形按边分有普通三角形(三条边都不相等),等腰三角(腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形);按角分有直角三角形、锐角三角形、钝角三角形等,其中锐角三角形和钝角三角形统称斜三角形。
斜边
斜边是指直角三角形中最长的那条边,也指不是构成直角的那条边。在勾股定理中,斜边称作“弦”。